因子2kdoe是一種實驗設計的方法，具有兩個級別(1/-1)的因子。
1.全因子2KDOE。
全因子2KDOE是DOE 實驗設計針對所有因子的方法。例如，如果有四個因素需要設計，2K=24=16次。
2.2K除法因子DOE。
部分2K因子DOE是對全因子DOE進行部分實驗的DOE。它進一步簡化了DOE實驗的次數，提高了工作效率，節約了實驗成本和新產品開發的實驗周期，為新產品定型和盡快進入市場提供了實驗方法。
正交試驗是采用標準正交表的多因素多水平試驗方法。也是優化測試方法之一，可以用較少的實驗次數找到最優的實驗條件，從而產生最優的設計方案，也是六西格瑪 design中常用的方法之一。
正交表
2.混合正交試驗
設計了既考慮關鍵因素又考慮一般因素的混合正交試驗。例如，L8(41×24)是一個因素的四個層次和四個因素的兩個層次的組合，是多個因素和多個層次的組合。常用的混合正交表有L18(61×36)、L8(41×24)、L16(43×26)、L32(49×24)和L12 (31
3.交互式正交試驗
正交試驗是一些因素相互作用的正交試驗。在一些正交試驗中，有些試驗結果是多因素綜合作用的結果，即一個因素對另一個因素有交互影響。對于這樣的正交實驗，需要選擇合適的正交表。
以下是L16(215)交互表。
響應面實驗是一種研究非線性關系和優化選擇變量的設計，常用于研究多水平變量。
兩個水平2K因子實驗無法估計曲線關系，不可能找到最優值。y和x的關系可能是一條曲線，所以用二項式方程更合適。
（1）單個變量的情況：
（2）兩個獨立變量的情況：
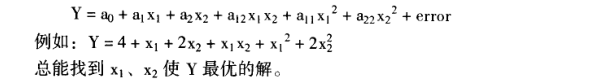
（3）三個獨立變量的情況：
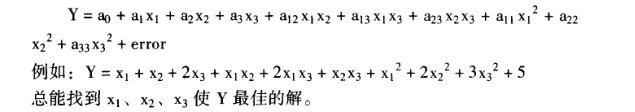
從上可知三水平響應曲面試驗是基于
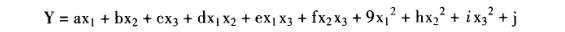
的數學模型進行響應曲面實驗。
應用minitab可方便地對三水平響應曲面實驗建模，并找到最優參數點。
五水平響應曲面試驗又叫中心合成設計（CCD），可以對5個水平的X變量進行檢驗，它是適用二次關系的最佳模型。
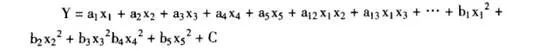
應用minitab可以方便地對五水平二次關系的數學模型進行優化求解。
全國服務熱線：
400-777-6907
天行健企業管理顧問有限公司 全國服務熱線：400-777-6907
郵箱：zyg@leanchina.cn 網址：www.pycity.com.cn
關注天行健微信
既獲取更多信息
版權所有@深圳市天行健企業管理顧問有限公司 粵ICP備13011693號
